Aufgabenstellung:
Es seien
Lösungsweg:
Drücke auf "Aufdecken" um dir den ersten Schritt der Lösung anzuzeigen
Geg.:
Ges.: Verteilung von
Offenbar gilt für die Verteilung von
Für die Bestimmung der Verteilung von
Für
Aus der folgenden Skizze kann dann das Ergebnis abgelesen werden (man betrachte die ensprechenden Flächeninhalte).
Skizze
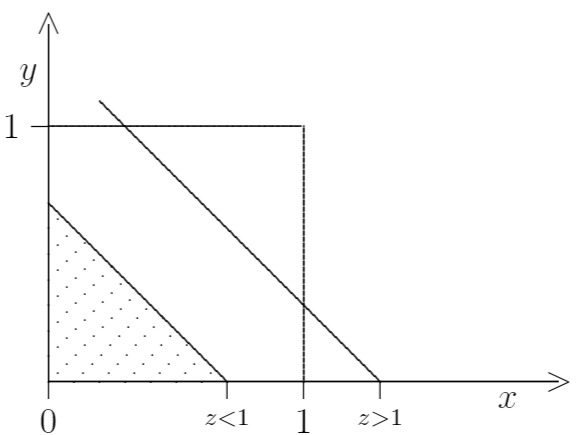
Damit erhält man
und
-
(Für das Integrationsgebiet muß jeweils gelten:
Die nachfolgende Skizze zeigt nochmals die Verteilungsdichten von
Skizze
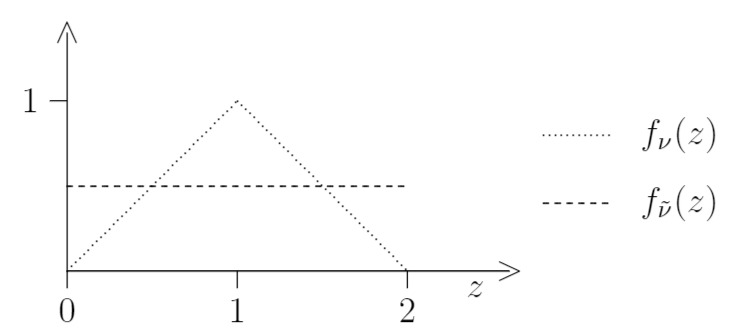
Lösung:
siehe Löungsweg