Leibnizkriterium

Theorie:

Leibnizkriterium

Es ist oft sinnvoll, das Leibnizkriterium zur Untersuchung einer Reihe auf Konvergenz zu benutzen, wenn ein alternierendes Vorzeichen wie z.B. besitzt. Da solche Reihen oft konvergieren, aber nicht absolut konvergieren, scheitern die anderen Konvergenzkriterien meistens.

Nutze zur Anwendung die folgenden Schritte:

Vorgehen

Leibnizkriterium

Die Konvergenz der alternierenden Reihe ist gezeigt, wenn eine monoton fallende Nullfolge ist. Zeige also:

ist eine Nullfolge, also:
ist monoton fallend, also:
Nutze zum Nachweis eine äquivalente Umformung

Tipps zur Grenzwertberechnung

Hinweis

Falls ein Bruch von der Form oder vorliegt:

Finde die größte Potenz von im Nenner und klammere diese in Zähler und Nenner aus. Kürze anschließend und schaue wo Nullfolgen entstanden sind.

Falls von der Form :

Nutze zunächst die Umformung um die Form zu erhalten. Nun kannst du obigen Tipp verwenden.

Falls von der Form :

Bringe den Ausdruck auf die Form und nutze anschließend, dass gilt

Leibniz-Kriterium

Das Leibniz-Kriterium ist ein spezielles Konvergenzkriterium für alternierende Reihen. Das sind Reihen, bei denen das Vorzeichen bei jedem Summanden wechselt, also Reihen der Form oder , wobei alle positiv sind. Da solche Reihen häufig konvergieren, aber nicht absolut konvergieren, scheitern die anderen Konvergenzkriterien oftmals.

Wie der Name schon vermuten lässt, wurde das Kriterium von dem Mathematiker Gottfried Wilhelm Leibniz im Jahre 1682 veröffentlicht. Übrigens wurde auch der Butterkeks mit seinen 52 Zähnen (in Anlehnung an die 52 Zahnräder der ersten von Leibniz entwickelten Rechenmaschine) nach ihm benannt.

Einstiegsbeispiel: Konvergenz der alternierenden harmonischen Reihe

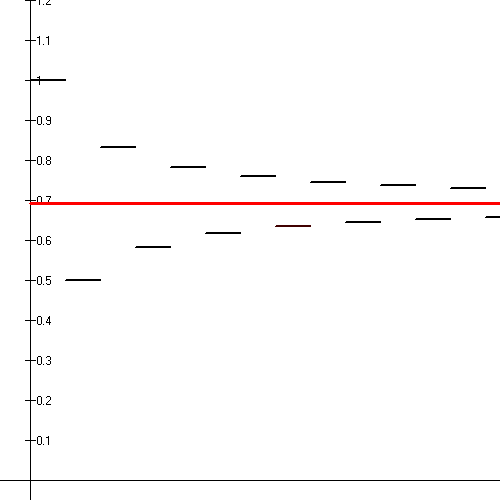
Da Beweisideen an konkreten Beispielen oftmals besser veranschaulicht werden können, betrachten wir zunächst das Beispiel der alternierenden harmonischen Reihe . Für die Konvergenz müssen wir zeigen, dass die Folge der Partialsummen konvergiert. Für haben die Partialsummen die Werte

Daran erkennen wir, dass die Werte in immer kleiner werdenden Schritten hin und her springen. Außerdem fällt auf, dass die Partialsummen mit ungeraden Indizes anscheinend monoton fallen und diejenigen mit geraden Indizes monoton wachsen. Dies können wir allgemein leicht nachrechnen. Für alle gilt nämlich

d.h. Und ganz analog , d.h. . Damit ist monoton fallend und monoton steigend.

Wenn wir zeigen könnten, dass nach unten und nach oben beschränkt sind, dann wären beide (Teil-)Folgen nach dem Monotoniekriterium konvergent. Nun sind aber alle ungeraden Partialsummen durch die geraden Partialsummen nach unten und umgekehrt alle geraden durch die ungeraden nach oben beschränkt, denn für alle gilt

und damit bzw. Insbesondere gilt daher und . Also ist nach unten durch und nach oben durch 1 beschränkt.

Nach dem Monotoniekriterium sind somit und konvergent.
Wir sind aber noch nicht fertig! Zum einen müssen wir zeigen, dass beide Teilfolgen gegen denselben Grenzwert konvergieren und zum anderen, dass daraus auch die Konvergenz von folgt.

Sei also und Wir müssen nun zeigen, dass beide Grenzwerte gleich sind, also dass gilt. Dies lässt sich aber schnell erledigen. Einerseits ist nämlich mit der Summenregel für Grenzwerte

Andererseits haben wir oben gezeigt. Damit ist nun

Also ist und daher .
Nun müssen wir noch zeigen, dass ebenfalls gegen konvergiert. Dazu müssen wir die Definition der Konvergenz benutzen, d.h. wir müssen zeigen

Wir wissen aber bereits

da ja und gegen denselben Grenzwert konvergieren. Setzen wir nun , so folgt unmittelbar

Verallgemeinerung der Beweisidee für das Leibniz-Kriterium

Die Frage ist nun, inwiefern wir den gerade geführten Beweis für die Konvergenz der alternierenden harmonischen Reihe verallgemeinern können, um ein allgemeines Konvergenzkriterium für alternierende Reihen zu erhalten. Dazu müssen wir uns klar machen, welche Eigenschaften der alternierenden harmonischen Reihe wir für den Konvergenzbeweis herangezogen haben.

Zum einen wissen wir, dass die nichtnegative Koeffizientenfolge ohne das alternierende Vorzeichen monoton fällt. Daraus hat sich dann die Monotonie und die Beschränktheit der beiden (Teil-)Partialfolgen und und damit deren Konvergenz ergeben.
Zum anderen haben wir davon Gebrauch gemacht, dass eine Nullfolge ist. Daraus konnten wir schließlich folgern, dass und und damit auch gegen denselben Grenzwert konvergieren.
Mehr Eigenschaften der alternierenden harmonischen Reihe hatten wir im Beweis oben nicht verwendet. Genau das sind auch die Voraussetzungen für das Leibniz-Kriterium:

Definition

Leibniz-Kriterium
Sei eine nichtnegative monoton fallende Folge reeller Zahlen mit , dann konvergiert die alternierende Reihe .

Anmerkungen zum Leibniz-Kriterium

Natürlich gilt das Leibniz-Kriterium auch für Reihen der Form . Denn diese unterscheiden sich nur durch die "umgedrehten" Vorzeichen. Der Beweis funktioniert ganz analog mit vertauschten Rollen von und .
Ebenso gilt es für Reihen der Form oder . Lass dich durch Indexverschiebungen nicht aus der Ruhe bringen!
Beachte, dass aus dem Leibniz-Kriterium nur die Konvergenz und nicht die absolute Konvergenz der Reihe folgt. Wie oben schon erwähnt, gibt es viele konvergente alternierende Reihen, die nicht absolut konvergieren. Ein Standardbeispiel ist wieder die alternierende harmonische Reihe .
Im Gegensatz zu manch anderem Konvergenzkriterium kann aus dem Leibniz-Kriterium nie die Divergenz einer Reihe gefolgert werden. Besitzt eine Reihe nicht alle Eigenschaften, die das Kriterium fordert, heißt das nicht, dass die Reihe divergieren muss. Das Leibniz-Kriterium ist in diesen Fällen nicht anwendbar.
Schließlich lässt sich das Leibniz-Kriterium erweitern auf den Fall, dass eine nicht-positive, monoton steigende Nullfolge ist. Der Beweis funktioniert ganz analog. Fassen wir beide Fälle zusammen, so konvergiert die Reihe , falls eine monotone Nullfolge ist.